ML-Ch2-P1-End to End Machine Learning Project

Introduction

Welcome to this exciting chapter! In this blog, I’ll work through an end-to-end machine learning project, turning raw data into actionable insights and a working model. Follow these structured steps to tackle any ML problem confidently.

---

The Roadmap: Steps to Build a Machine Learning Project

Here’s are the main steps:

1. Look at the Big Picture
2. Get the Data
3. Explore and Visualize the Data to Gain Insights
4. Prepare the Data for Machine Learning Algorithms
5. Select a Model and Train It
6. Fine-Tune the Model
7. Present the Solution
8. Launch, Monitor, and Maintain the System

---

Working with Real Data

To work on real-world problems, you’ll need real data. Here’s where to find it:

Popular Open Data Repositories:

• OpenML.org
• Kaggle.com
• PapersWithCode.com
• UC Irvine Machine Learning Repository
• Amazon AWS Datasets
• TensorFlow Datasets

Meta Portals (they list open data repositories):

• DataPortals.org
• OpenDataMonitor.eu

Other Pages Listing Popular Open Data Repositories:

• Wikipedia’s List of Machine Learning Datasets
• Quora Discussions on Datasets
• The Datasets Subreddit

---

Step 1: Look at the Big Picture

Task: Use California census data to build a model predicting housing prices in the state.
Data: The dataset includes metrics such as population, median income, and median housing prices for each block group in California.

Frame the Problem:

• Type: Supervised learning
• Goal: Regression task (multiple regression and univariate regression)
• Approach: Batch learning

Select a Performance Measure:

A common performance measure for regression problems is the Root Mean Square Error (RMSE):

$$
\text{RMSE}(\mathbf{X}, \mathit{h}) = \sqrt{\frac{1}{m} \sum_{i=1}^m \left(h(\mathbf{x}^{(i)}) - y^{(i)}\right)^2}
$$

Check the Assumptions

For example, what kind of machine learning system you would like your data to be fed into, a classification or regression system?

---

Step 2: Get the Data

from pathlib import Path
import pandas as pd
import tarfile
import urllib.request

def load_housing_data():
    tarball_path = Path("Datasets/housing.tgz")
    if not tarball_path.is_file():
        Path("datasets").mkdir(parents=True, exist_ok=True)
        url = "https://github.com/ageron/data/raw/main/housing.tgz"
        urllib.request.urlretrieve(url, tarball_path)
        with tarfile.open(tarball_path) as housing_tarball:
            housing_tarball.extractall(path="datasets")
    return pd.read_csv(Path("datasets/housing/housing.csv"))

Question for myself:
The author mentions that there are 20,640 instances in the dataset. While this may seem small by machine learning standards, it’s perfect for getting started. How can we determine whether a dataset is “small” or not?

Get a feel of the type of the data!!!

1. using methods

housing = load_housing_data()
housing.head()
housing.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 20640 entries, 0 to 20639
Data columns (total 10 columns):
 #   Column              Non-Null Count  Dtype
---  ------              --------------  -----
 0   longitude           20640 non-null  float64
 1   latitude            20640 non-null  float64
 2   housing_median_age  20640 non-null  float64
 3   total_rooms         20640 non-null  float64
 4   total_bedrooms      20433 non-null  float64
 5   population          20640 non-null  float64
 6   households          20640 non-null  float64
 7   median_income       20640 non-null  float64
 8   median_house_value  20640 non-null  float64
 9   ocean_proximity     20640 non-null  object
dtypes: float64(9), object(1)
memory usage: 1.6+ MB

>>> housing["ocean_proximity"].value_counts()
ocean_proximity
<1H OCEAN     9136
INLAND        6551
NEAR OCEAN    2658
NEAR BAY      2290
ISLAND           5
Name: count, dtype: int64

>>> housing.describe()

output:

          longitude      latitude  housing_median_age  ...    households  median_income  median_house_value
count  20640.000000  20640.000000        20640.000000  ...  20640.000000   20640.000000        20640.000000
mean    -119.569704     35.631861           28.639486  ...    499.539680       3.870671       206855.816909
std        2.003532      2.135952           12.585558  ...    382.329753       1.899822       115395.615874
min     -124.350000     32.540000            1.000000  ...      1.000000       0.499900        14999.000000
25%     -121.800000     33.930000           18.000000  ...    280.000000       2.563400       119600.000000
50%     -118.490000     34.260000           29.000000  ...    409.000000       3.534800       179700.000000
75%     -118.010000     37.710000           37.000000  ...    605.000000       4.743250       264725.000000
max     -114.310000     41.950000           52.000000  ...   6082.000000      15.000100       500001.000000

[8 rows x 9 columns]

2. plotting histograms

import matplotlib.pyplot as plt

housing.hist(bins=50, figsize=(12, 8))
plt.show()

Figure 1: This figure shows the distribution of housing prices in California, with data grouped by region and income levels.

Create a test set

Creating a test set is theoretically simple; pick some instances randomly, typically 20% of the dataset (or less if your dataset is very large), and set them aside:

def shuffle_and_split_data(data, test_ratio):
  shuffled_indices = np.random.permutation(len(data))
  test_set_size = int(len(data) * test_ratio)
  test_indices = shuffled_indices[:test_set_size]
  train_indices = shuffled_indices[test_set_size:]
  return data.iloc[train_indices], data.iloc[test_indices]

then we can use the function to get the test set:

>>> train_set, test_set = shuffle_and_split_data(housing, 0.2)
>>> len(train_set)
16512
>>> len(test_set)
4128

the problem is: once we run the program again, it will generate a different test set. Over time, we will get to see the whole dataset.
solution:

• to save the test set on the first run and then load it in subsequent runs.
• to set the random number generator’s seed (using np.random.seed(42)) before calling np.random.permutation() so it always generates the same shuffled indices.
  another problem comes: above solutions will break the next time we fetch an updated dataset.
  solution: to have a stable train/test split even after updating the dataset, a common solution is to use each instance’s identifier to decide whether or not it should go in the test set. For example, to compute a hash of each instance’s identifier and put that instance in the test set if the hash is lower than or equal to 20% of the maximum hash value. This ensures that the test set will remain consistent across multiple runs, even if we refresh the dataset.

from zlib import crc32

def is_id_in_test_set(identifier, test_ratio):
  return crc32(np.int64(identifier)) < test_ratio * 2**32

def split_data_with_id_hash(data, test_ratio, id_column):
  ids = data[id_column]
  in_test_set = ids.apply(lambda id_: is_id_in_test_set(id_, test_ratio))
  return data.loc[~in_test_set], data.loc[in_test_set]

Scikit-Learn provides a few functions to split datasets into multiple subsets in various ways.

• The simplest function is train_test_split(), which does pretty much the same thing as the shuffle_and_split_data() function.
  • there is a random_state parameter that allows us to set the random generator seed
  • we can pass it multiple datasets with an identical number of rows, and it will split them on the same indices

    from sklearn.model_selection import train_test_split
    
    train_set, test_set = train_test_split(housing, test_size = 0.2, random_state=42)

How to avoid sampling bias?

• we should not have too many strata, and each stratum should be large enough
  e.g.
• some experts told us that the median income is a very important attribute to predict median housing prices
• then we want to ensure that the test set is representative of the various categories of incomes in the whole dataset
• so we try to categories the data
  method 1:

housing["income_cat"] = pd.cut(housing["median_income"],
                                       bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
                                       labels=[1, 2, 3, 4, 5])
                              
housing["income_cat"].value_counts().sort_index().plot.bar(rot=0, grid=True)
plt.xlabel("Income category")
plt.ylabel("Number of districts")
plt.show() 

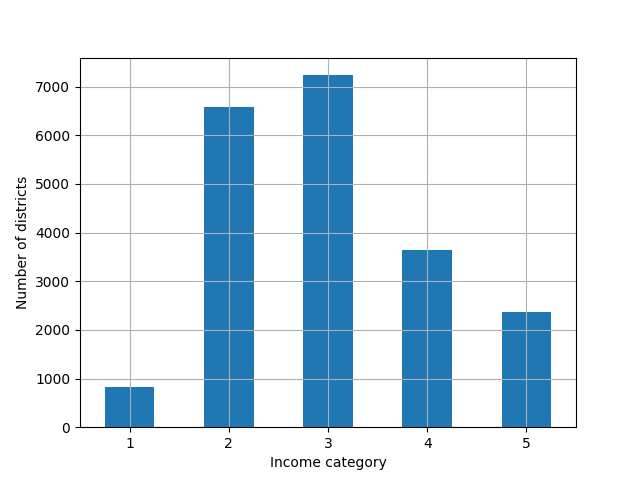
Figure 2: Histogram of income categories using pd.

method 2: using multiple splits

from sklearn.model_selection import StratifiedShuffleSplit

splitter = StratifiedShuffleSplit(n_splits=10, test_size=0.2, random_state=42)
strat_splits = []
for train_index, test_index in splitter.split(housing, housing["income_cat"]):
  strat_train_set_n = housing.iloc[train_index]
  strat_test_set_n = housing.iloc[test_index]
  strat_splits.append([strat_train_set_n, strat_test_set_n])

we can just the first split

strat_train_set, strat_test_set = strat_splits[0]

then

>>> strat_test_set["income_cat"].value_counts() / len(strat_test_set)
income_cat
3    0.350533
2    0.318798
4    0.176357
5    0.114341
1    0.039971
Name: count, dtype: float64